Wir nähern uns einem interessanten, aber auch anspruchsvollen Thema: Wie genau messen unsere Ohren eigentlich? Und in diesem Zusammenhang: Was ist ein „absolutes“ Gehör? Und was ist ein „relatives Gehör“? Wie klein ist unsere Frequenz-Unterschieds-Schwelle?
Unsere Ohren haben messtechnische Fähigkeiten, die uns immer wieder in Erstaunen versetzen! Lassen Sie sich faszinieren und verzaubern!
Die Funktionsweise des Innenohres habe ich schon an anderer Stelle beschrieben.
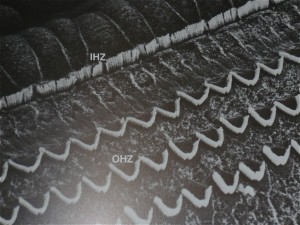
1 Reihe innerer Haarzellen (IHZ) und 3 Reihen äußerer Haarzellen (OHZ)
Nebeneinander liegende Gruppen (Kaskaden) bestehen aus je einer inneren und drei äußeren Haarzellen
Wir haben bereits erfahren, dass es auf der Basilarmembran des Innenohres etwa 5000 Gruppen („Kaskaden“) gibt, die aus je drei äußeren und einer inneren Haarzelle bestehen. Jede dieser Kaskaden ist für eine andere Tonhöhe zuständig. Töne, die auf zwei unterschiedliche Kaskaden „fallen“, werden als unterschiedlich hoch wahrgenommen.
Das bedeutet: Wir sind in der Lage, unseren gesamten hörbaren Tonhöhenbereich in 5000 Feinabstufungen zu unterteilen! Das scheint eine ziemlich feine Feinabstufung zu sein.
Es ist tatsächlich eine sehr feine Feinabstufung! Lassen Sie sich überraschen!
Um diese Fähigkeit richtig abschätzen zu können, müssen wir einen weiten Bogen spannen und ein wenig in physikalische und musikalische Grundlagen eintauchen. Aber es lohnt sich!
Bekanntlich hat sich schon Pythagoras mit Musik beschäftigt – neben seiner bekannten Haupttätigkeit als Mathematiker. Und was kommt dabei heraus, wenn sich ein Mathematiker mit Musik beschäftigt? Es kommen mathematische Gesetze der Musik dabei heraus! Tatsächlich gehörte die Musik im Mittelalter – natürlich lange nach Pythagoras! – zu den „sieben freien Künsten“ – und zwar im engeren Sinne zu den vier mathematischen „Künsten“ („Quadruvium“: Arithmetik, Geometrie, Astronomie und Musik). Die drei übrigen „Künste“ waren sprachlicher Natur („Trivium“: Rhetorik, Grammatik und Dialektik). Übrigens: Auch damals schon fand man die mathematischen Künste anspruchsvoller. Die drei sprachlichen Künste des Triviums waren im Gegensatz zu den vier mathematischen Künsten des Quadruviums eben „trivial“ … Das Wort gebrauchen wir heute noch mit praktisch gleicher Bedeutung …
Pythagoras hat mit einer Saite experimentiert. Hat er die Saite angezupft, erklang ein Ton (das ist heute noch genauso!). Die Tonhöhe war offenbar abhängig von der Länge der Saite: kurze Saiten produzierten hohe Töne, lange Saiten tiefe Töne. Und Pythagoras hat festgestellt, dass die Zahl der Schwingungen („Frequenz“) einer Saite umgekehrt proportional ist zu ihrer Länge. Doppelte Länge heißt halbe Frequenz und umgekehrt.
Und noch etwas hat Pythagoras beobachtet. Spannt man eine Saite an beiden Enden fest ein und zupft sie an, dann entsteht nicht nur eine Schwingung („Grundton“) über die ganze Länge der Seite! Es gibt auch eine weitere, schwächere Schwingung, die der ersten überlagert ist und die genau auf halber Länge einen „Schwingungknoten“ hat. Dieser Schwingungsknoten schwingt selbst gar nicht mit (nur mit der „unterlagerten“ Grundfrequenz), aber sorgt dafür, dass die beiden durch den Schwingungsknoten in der Mitte geteilten Saitenhälften eben ganz genau die halbe Länge und die doppelte Frequenz aufweisen! Es ist der erste Oberton mit doppelter Tonhöhe wie der Grundton! Hat der Grundton die Frequenz „f“, dann hat der erste Oberton die Frequenz „2f“. Die doppelte Frequenz empfindet unser Ohr musikalisch als eine „Oktave“ (8 Töne einer Tonleiter). Die Oktave (die doppelte Frequenz) ist für unser Ohr so nah verwandt, dass die frühen Musiker den jeweiligen Oktaven die gleichen Notennamen zugeteilt haben. Diese Namen haben auch heute noch Gültigkeit!
Aber das ist noch nicht alles, was Pythagoras entdeckt hat: Neben einer Oberschwingung mit 2f gibt es auch noch Oberschwingungen mit 3f, 4f, 5f, 6f, 7f, 8f, 9f usw. Dabei ist jede höhere Oberschwingung leiser als die unmittelbar tiefere Oberschwingung. Alle Oberschwingungen zusammen bilden die „Klangfarbe“ des Tones.
Nicht jedes Musikinstrument bildet gleichermaßen alle Obertöne. Das Muster an fehlenden und vorhandenen Obertönen und deren relativen Lautstärken bestimmt die charakteristische Klangfarbe eines Instrumentes.
Spielt man einen Grundton und mehrere seiner Obertöne hintereinander, so erhält man die sogenannte „Naturtonreihe“. Die Intervalle aller Naturtonreihen sind gleich, auch wenn der Grundton wechselt, aber innerhalb einer jeden Reihe werden die Intervalle zu den hohen Tönen hin immer enger! Das Schwingungsverhältnis zweier aufeinanderfolgender Töne (2:1, 3:2, 4:3, 5:4, 6:5, 7:6, 8:7 …) wird mit jedem Schritt kleiner. Schließlich geht es immer um ganzzahlige Vielfache der Grundfrequenz. Nicht-ganzzahlige Vielfache können physikalisch gar nicht vorkommen, da beide Enden der Saite eingespannt und die Länge der Saite damit fest vorgegeben ist. Die Zahl der Schwingungsknoten ist immer ganzzahlig! Einen „halben Knoten“ gibt es nicht…
Man kann jeden beliebigen Ton zum Grundton einer Naturtonreihe machen. Allerdings: Je tiefer der gewählte Ton ist, desto mehr Obertöne kann man spielen, bevor die Tonhöhe in für unsere Ohren unhörbare Höhen entschwindet. Aus diesem Grund sind Alphörner so lang …
Spielt man also den zweiten Ton der Reihe, liegt dieser bereits eine ganze Oktave oberhalb des Grundtones: Das Verhältnis beider Töne ist 2:1 (=2). Spielt man den 3. Ton der Reihe, liegt dieser nur noch eine Quinte (5 Töne) über dem 2. Ton und das Frequenzverhältnis verkleinert sich auf 3:2 (=1,5). Mit dem nächsten Ton erreicht man die Quarte (4 Töne) mit 4:3 (≈ 1,33). Dieser Ton liegt jetzt 1 Oktave über dem 2. Ton der Reihe, nämlich 4:2 (kann auf 2:1 = 2 gekürzt werden) und zugleich 2 Oktaven über dem Grundton, nämlich 2 x (2:1) = 4:1. An dieser Stelle sei verraten, dass alle Frequenzen, deren Verhältnisse zum Grundton Zweierpotenzen entsprechen, immer im ein- oder mehrfachen Oktavabstand zum Grundton erklingen.
Es folgen weitere Intervalle: große Terz mit 5:4, kleine Terz mit 6:5, große Sekunde mit 7:6 und kleine Sekunde mit 8:7. Und wir haben wieder einen weiteren Oktav-Abstand zum Grundton gewonnen: 8 ist gleich 2 hoch 3 (= 2 x 2 x 2). Wir liegen nun 3 Oktaven über dem Grundton.
Bis hierher ist eigentlich alles noch ganz schön und relativ einfach. Die Frequenzverhältnisse sind ganzzahlig und Zweierpotenzen sind auch relativ einfach auszurechnen.
Man kann aber nicht nur durch fortwährendes Verdoppeln der Frequenz (also Oktave folgt auf Oktave) auf einen gleichnamigen Ton einer viel höheren Oktavlage kommen, sondern auch durch fortwährendes Aneinanderreihen von Quinten – eigentlich sogar durch Aneinanderreihen von 12 beliebigen, aber jeweils immer gleichen, Intervallen. In einer Oktave finden sich zwölf unterschiedliche Halbtöne mit jeweils eigenen Notennamen. Wenn man also 12 Quinten aufeinander schichtet, kommt jeder Halbton einmal vor und man erreicht musikalisch den gleichen Ton, den man durch Aufschichtung von 7 Oktaven erreicht hätte. Das lässt sich sehr schön am sogenannten „Quintenzirkel“ veranschaulichen. Okay – der Begriff „musikalisch gleicher Ton“ stimmt nicht so ganz. Er gilt eigentlich nur für Musikinstrumente mit festen Tönen (Tasten, Klappen …), die man enharmonisch verwechseln kann.
Konkret sieht das so aus:
7 Oktaven aufeinander geschichtet:
(Start = Subkontra C), Kontra C, C, c, c’, c’’, c’’’, c’’’’ – 7 Oktaven. Das Frequenzverhältnis beträgt demnach (2 hoch 7) zu 1 = 128 : 1 = 128.
Und jetzt die Schichtung von 12 Quinten:
(Start = Subkontra C), Subkontra G, Kontra D, Kontra A, E, H, fis, cis’, gis’, dis’’, ais’’, eis’’’, his’’’. Das his’’’ liegt einen halben Ton über (deshalb die Endung –is) dem h’’’ und ist damit enharmonisch zugleich das c’’’’. Wir sind also musikalisch beim gleichen Ton angekommen wie in der oberen Reihe nach 7 Oktaven. Das Frequenzverhältnis beträgt demnach also (3:2 hoch 12) zu 1, entsprechend (1,5 hoch 12) zu 1, was ausgerechnet ungefähr 129,746337890625 : 1 ist – also 129,746337890625.
Hoppla! Was ist jetzt passiert?
Gehen wir vom Grundton aus 7 Oktaven nach oben, dann ist die Frequenz 128 mal höher. Gehen wir aber 12 Quinten nach oben, dann landen wir auf dem enharmonisch selben Ton, die Frequenz ist aber etwa 129,75 mal höher. Das passt nicht zusammen! Zwölf Quinten sind offensichtlich mehr als 7 Oktaven. Und das ist ein Problem, das die Musik von Anfang an begleitet hat.
Diesen Unterschiedsbetrag nennt man das „pythagoräische Komma“.
Immer wieder haben Instrumentenbauer und Musiker versucht, dieses pythagoräische Komma geschickt mehr oder weniger gleichmäßig auf die Intervalle zu verteilen. Es gibt viele „Stimmungssysteme“, darunter bekannte wie z. B. die „mitteltönige Stimmung“, die „Kirnberger-Stimmungen“ und die „Werckmeister-Stimmungen“.
Solange die Verteilung des „Überschusses“ ungleichmäßig auf die Intervalle verteilt wird, erhält man eine sogenannte Tonartencharakteristik: Man kann hören, ob die Tonart nah bei C-Dur oder weit entfernt von C-Dur liegt! Obwohl es unter Musikwissenschaftlern unterschiedliche Meinungen darüber gibt, ob die Tonartencharakteristik von früheren Komponisten wie z. B. Johann Sebastian Bach erwünscht oder unerwünscht war, scheint es doch ziemlich fest zu stehen, dass J. S. Bach letztendlich eine gleichmäßige Verteilung auf alle Intervalle wünschte. Eine gleichmäßige Verteilung nennt man auch eine gleichstufige Stimmung. Die gleichstufige Stimmung ist eine „wohltemperierte“ Stimmung. Allerdings sind nicht alle „wohltemperierten“ Stimmungen auch gleichstufig. Die Werckmeisterstimmungen sind wohltemperiert, aber nicht gleichstufig. Nur die gleichstufige, wohltemperierte Stimmung erlaubt es, in jeder Tonart zu komponieren, was J. S. Bach auch gleich voller Tatendrang praktizierte: Im „Wohltemperierten Klavier“ finden sich Präludien und Fugen in jeder Tonart. Obwohl J. S. Bach die gleichstufige Stimmung nicht explizit im Titel angegeben hat, darf man davon ausgehen, dass er sie meinte: Nur auf einem gleichstufig wohltemperierten Klavier lassen sich nämlich alle Stücke aus dem Büchlein spielen!
Wenn in einer Oktave 12 Halbtöne liegen und das Frequenzverhältnis von 2:1 gleichstufig auf 12 Halbtöne verteilt werden muss, sodass sich nicht etwa 12 gleiche Differenzen, sondern 12 gleiche Verhältnisse ergeben, dann gibt es nur eine Lösung: Ein gleichstufig gestimmter Halbton steht zu seinem Nachbarn immer im Verhältnis von „zwölfter Wurzel aus zwei“ zu eins (1,05946… :1)
Für einen normalen Musikgebrauch reicht diese Angabe aus. Wenn man aber Feinabstimmungen vornehmen will (z. B. als Klavier-, Cembalo- oder Orgelstimmer), dann braucht man kleinere Intervalle. Wir arbeiten schon seit vielen Jahren mit dem Dezimalsystem, da bietet es sich geradezu an, einen Halbton zusätzlich noch in hundert hundertstel Halbtöne zu teilen. Vorsicht: Das Wort „teilen“ deutet eine Division in gleiche Differenzen an, aber das wäre falsch! Bekanntlich sind für die musikalischen Belange (siehe oben) nicht Frequenzdifferenzen entscheidend, sondern Frequenzverhältnisse! Auch hier müssen wir wieder mit Wurzeln arbeiten. Na ja, zu Zeiten von Taschenrechnern kein Problem.
Ein hundertstel Halbton wird auch „Cent“ genannt. Und ein hundertstel Halbton (Cent) steht zu seinem Nachbar-Hundertstel-Halbton immer im Verhältnis von „eintausendzweihundertster Wurzel aus 2“ zu eins (nämlich 12 Halbtöne mal 100 = 1200). Mein Taschenrechner sagt, das sei ungefähr 1,0005777… :1. Er muss es ja wissen … Eine ganze Oktave hat also 1200 Cent: 12 Halbtöne zu je 100 Cent.
Das Rechnen mit den Cents ist wieder einfach. Da reichen die 4 Grundrechenarten aus. Und die Centwerte sind praktisch immer klein. Also kein Problem.
Jetzt kümmern wir uns mal um das pythagoräische Komma (siehe oben). Das Frequenzverhältnis beträgt etwa 129,75:128 entsprechend 1,0117. Wenn wir wissen wollen, wie viel Cent das sind, dann müssen wir eine Zahl finden, mit der wir die zwölfhundertste Wurzel aus 2 (= 1,0005777) potenzieren müssen, damit 1,0117 dabei heraus kommt. Mathematisch ausgedrückt suchen wir also den Logarithmus von 1,0117 zur Basis 1,0005777. Dank unserer kleinen Rechenknechte – und mit etwas Wissen – kommt man schnell zum Ergebnis: ungefähr 24. Diese 24 Cent müssen bei der wohltemperierten Stimmung auf 12 Quinten verteilt werden. Auch das ist leicht: Jede „wohltemperiert Quinte“ ist um 2 Cent (24/12) kleiner als die „reine“ Quinte (12 reine Quinten sind um 24 Cent größer als 12 wohltemperierte Quinten = 7 Oktaven – eben um das pythagoräische Komma). Um bei der Quinte (= 7 Halbtöne) zu bleiben: Die wohltemperierte Quinte hat 700 Cent, die reine Quinte 702 Cent. – Ich möchte das gern mal am Beispiel einer Uhr verdeutlichen, die ja auch 12 Teilstriche auf ihrem Zifferblatt hat, ein Strich für 5 Minuten. Wenn man bei 12 Uhr startet und dreht den Minutenzeiger einmal um einen vollen Kreis (entsprechend 7 „Oktaven“), dann steht der Minutenzeiger wieder oben. Es sind 3.600 Sekunden vergangen. Dreht man den Minutenzeiger aber immer um einen Teilstrich weiter, dann sollte er nach 12 dieser 5-Minutenschritte (entsprechend 12 „Quinten“) auch wieder oben stehen. In unserem Vergleichsbeispiel wäre das dann aber nicht so. Nach 12 der 5-Minutenintervalle (12 „Quinten“) wären dann 3.649,116 Sekunden vergangen und der Minutenzeiger dementsprechend um 49,116 Sekunden (das entspricht 24 Cent) weiter fortgeschritten als er eigentlich sollte. Jedes „reine“ 5-Minuten-Intervall wäre um 4,093 Sekunden (entsprechend 2 Cent) größer als ein „wohltemperiertes“ 5-Minuten-Intervall (304,093 Sekunden anstatt 300 Sekunden). – Übrigens: Alle Halbtöne einer gleichstufig wohltemperierten Stimmung haben immer Centbeträge, die genau ganzzahlige Vielfache von 100 sind (so ist die Einheit ja definiert: ein hundertstel Halbton – und zwar ein Hundertstel eines gleichstufig temperierten Halbtons).
Zurück zum pythagoräischen Komma – 24 Cent – und seinen Verteilungsproblemen. Man kann jetzt nämlich für jedes beliebige Intervall ausrechnen, um wie viel Cent sich das „reine Intervall“ vom entsprechenden „wohltemperierten Intervall“ unterscheidet. Kann man. Muss man aber nicht – zumindest nicht an dieser Stelle. Dieses Spezialwissen ist zum Beispiel wichtig für gute Chöre, gute Streich- oder gute Posaunenquartette. Neben der menschlichen Stimme sind nur Streicher und Posaunen in der Lage, stufenlos die Tonhöhe zu ändern. Mit dem Wissen um die reinen Intervalle – und mit ganz viel Übung und Können! – können sie in „reiner Stimmung“ singen oder spielen, was einen ständigen Wechsel in der Intonation bedeutet! Um das mal in einem Beispiel zu verdeutlichen: Ein „c“ in C-Dur intoniert man nach der Stimmgabel. Ein „c“ als Quinte von F muss man um 2 Cent höher intonieren (702 anstatt 700 Cent). Ein „c“ als große Terz in As-Dur muss man um 14 Cent tiefer intonieren (386 Cent anstatt 400 Cent) und ein „c“ als kleine Terz in a-moll muss man um 16 Cent höher intonieren (316 Cent anstatt 300 Cent). Wie wäre es mit etwas Respekt den guten Musikern gegenüber? Jetzt habe ich die wichtigsten Intervalle doch noch genannt …
Der Vollständigkeit halber sei noch folgendes erwähnt:
Wenn man 2 reine Ganztöne übereinanderschichtet (C, D, E), erhält man keine reine Terz. Den Unterschied nennt man „syntonisches Komma„.
Wenn man 3 reine Großterzen übereinanderschichtet (C, E, Gis, c), erhält man keine reine Oktave, sondern ein kleineres Intervall. Den Unterschied nennt man „kleine Diesis„.
Wenn man 4 reine Kleinterzen übereinanderschichtet (C, Es, Ges, A, c), erhält man ebenfalls keine reine Oktave, sondern ein größeres Intervall. Den Unterschied nennt man „große Diesis„.
Wir wenden uns jetzt wieder unseren Ohren zu. Eine interessante Frage ist, welchen Frequenzbereich können wir – ungefähr – wahrnehmen? Wenn man schon ein paar Jährchen hinter sich gebracht hat, dann liegt der Bereich etwa zwischen 18 Hz und 18.000 Hz. Das sind ungefähr 10 Oktaven. In Cent ausgedrückt: 12.000 Cent (10 Oktaven zu je 12 Halbtönen zu je 100 Cent). Für diesen Bereich stehen uns auf der Basilarmembran etwa 5000 Kaskaden zur Verfügung (siehe oben). Unsere Frequenzunterschiedsschwelle beträgt also ziemlich genau 2,4 Cent pro Kaskade (12000 Cent dividiert durch 5000 Kaskaden). Gesunde Ohren können unterschiedliche Tonhöhen wahrnehmen, wenn die Tonhöhen sich um nur 2,4 Cent unterscheiden! Das ist eine große Leistungsfähigkeit unserer Ohren! Und das ist auch die Antwort auf die Frage oben, wie fein unsere Feinabstimmung tatsächlich ist! Wenn man das auf einem Klavier realisieren wollte, müsste man aus jeder Klaviertaste (= 100 Cent) knapp 42 Tasten zu je 2,4 Cent aussägen! Niemand kann das spielen! Aber mit Übung und Erfahrung kann man es hören! Unsere Ohren bieten uns alle Möglichkeiten dazu!
Wohlgemerkt: Dieser Wert gilt für Töne, die nacheinander gespielt werden! Bei gleichzeitig gespielten Tönen können wir zusätzlich noch Schwebungen hören, an denen wir die Tonhöhenunterschiede auch erkennen können. Da ändert sich die Empfindlichkeit allerdings mit der Tonhöhe. Aber das ist wieder eine andere Geschichte …
Geübte Menschen können das Intervall benennen, wenn sie zwei Töne hören. Das ist für Musiker – für jeden Menschen nach einem entsprechenden Unterricht in „Gehörbildung“ – relativ einfach, da lediglich Frequenzverhältnisse erkannt werden müssen. Töne mit z. B. 2000 Hz und 3000 Hz bilden eine Quinte. Aber auch Töne von 200 Hz und 300 Hz stehen im Quintverhältnis. Und Töne von 400 Hz und 600 Hz: Alles Quinten im Verhältnis 3:2.
Wenn man „gehörgebildeten“ Menschen einen Ton als Bezugspunkt vorgibt und dann einen anderen Ton spielt, dann können sie ziemlich schnell und treffsicher sagen, um welches Intervall es sich handelt. Und wenn man den ersten Ton mit Namen benennt, dann kann der Kandidat – über die Kenntnis des Intervalls – auch rasch den Namen des zweiten Tones sagen. Diese Fähigkeit nennt man: „relatives Gehör“. Man findet leicht Intervalle und Tonnamen relativ zu einem Bezugston. Alle guten Musiker haben ein gutes relatives Gehör. Es ist gewissermaßen eine Grundbedingung und wird dementsprechend an den Musikhochschulen gelehrt – und geprüft.
 Aber es gibt noch eine kleine Gruppe von Menschen, die können sogar eine einzelne Note mit Namen benennen ohne Bezugston. Wenn man ihnen eine einzelne Note – sozusagen frei im Raum schwebend – vorspielt, dann sagen sie wie die Note heißt! Wer das kann, der hat ein „absolutes Gehör“! Diese Fähigkeit ist absolut faszinierend und lässt tief blicken in die Wunderwelt unserer Ohren und Gehirne!
Aber es gibt noch eine kleine Gruppe von Menschen, die können sogar eine einzelne Note mit Namen benennen ohne Bezugston. Wenn man ihnen eine einzelne Note – sozusagen frei im Raum schwebend – vorspielt, dann sagen sie wie die Note heißt! Wer das kann, der hat ein „absolutes Gehör“! Diese Fähigkeit ist absolut faszinierend und lässt tief blicken in die Wunderwelt unserer Ohren und Gehirne!
Manche Menschen mit absolutem Gehör leiden aber gelegentlich unter dieser Fähigkeit. Wenn sie ein Gesangsstück – z. B. in C-Dur – im Notenblatt verfolgen und hören, dass der Chor nicht in C-Dur, sondern in Deses-Dur (also 24 Cent tiefer) singt, dann bekommen sie „die Krise“! C-Dur sehen und Deses-Dur hören sind zwei Welten für diese Menschen – obwohl der Unterschied von 24 Cent für Ungeübte und nicht mit dem absoluten Gehör begabte Menschen nicht wahrgenommen werden kann.
Was soll ich dazu sagen? Solch ein Luxusproblem hätte ich auch mal gern … Nein, ich will nicht lästern: Unter geringfügig falschen Tönen zu leiden, heißt häufig und viel zu leiden! Auch wenn wir „Normalos“ uns das nicht vorstellen können!



